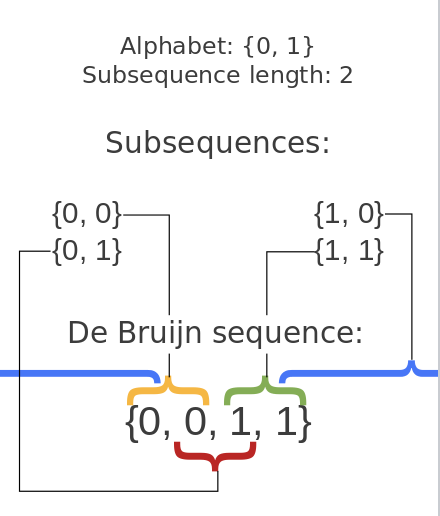
De Bruijn Sequence
In combinatorial mathematics, a de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring (i.e., as a contiguous subsequence). Such a sequence is denoted by B(k, n) and has length kn, which is also the number of distinct substrings of length n on A; de Bruijn sequences are therefore optimally short.
Applications
The sequence can be used to shorten a brute-force attack on a PIN-like code lock that does not have an "enter" key and accepts the last n digits entered. For example, a digital door lock with a 4-digit code would have B (10, 4) solutions, with length 10000. Therefore, only at most 10000 + 3 = 10003 (as the solutions are cyclic) presses are needed to open the lock. Trying all codes separately would require 4 × 10000 = 40000 presses.