Two Pointers
dp or Array Search
Often use two pointers to traverse the array, linked list, find dp solution ...
(ptr1)99999(ptr2)
List Length Cut into 2 Half
//when fast stops, slow is approximately at the middle of the list
ListNode fast=head.next, slow=head;
while(fast!=null && fast.next!=null) {
slow = slow.next;
fast = fast.next.next;
}
LinkedList Off-set
19. Remove Nth Node From End of List
First fast ptr goes forward by n off-set. When fast finishes, slow is n off-set from tail.
**use a dummy node to help with the traversal**
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if(head==null || n ==0) return head;
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode slow=dummy, fast=dummy;
for(int i=0; i<=n; i++)
fast = fast.next;
while(fast!=null) {
slow = slow.next;
fast = fast.next;
}
slow.next = slow.next.next;
return dummy.next;
}
}
Cycle Detection
One slow pointer, one fast pointer, they will meet if there is a cycle.
Below prove s+m = nr, which means if we start one pointer at the point where they meet, and travel s steps, it will be nr, which means it will stop at the start of the cycle.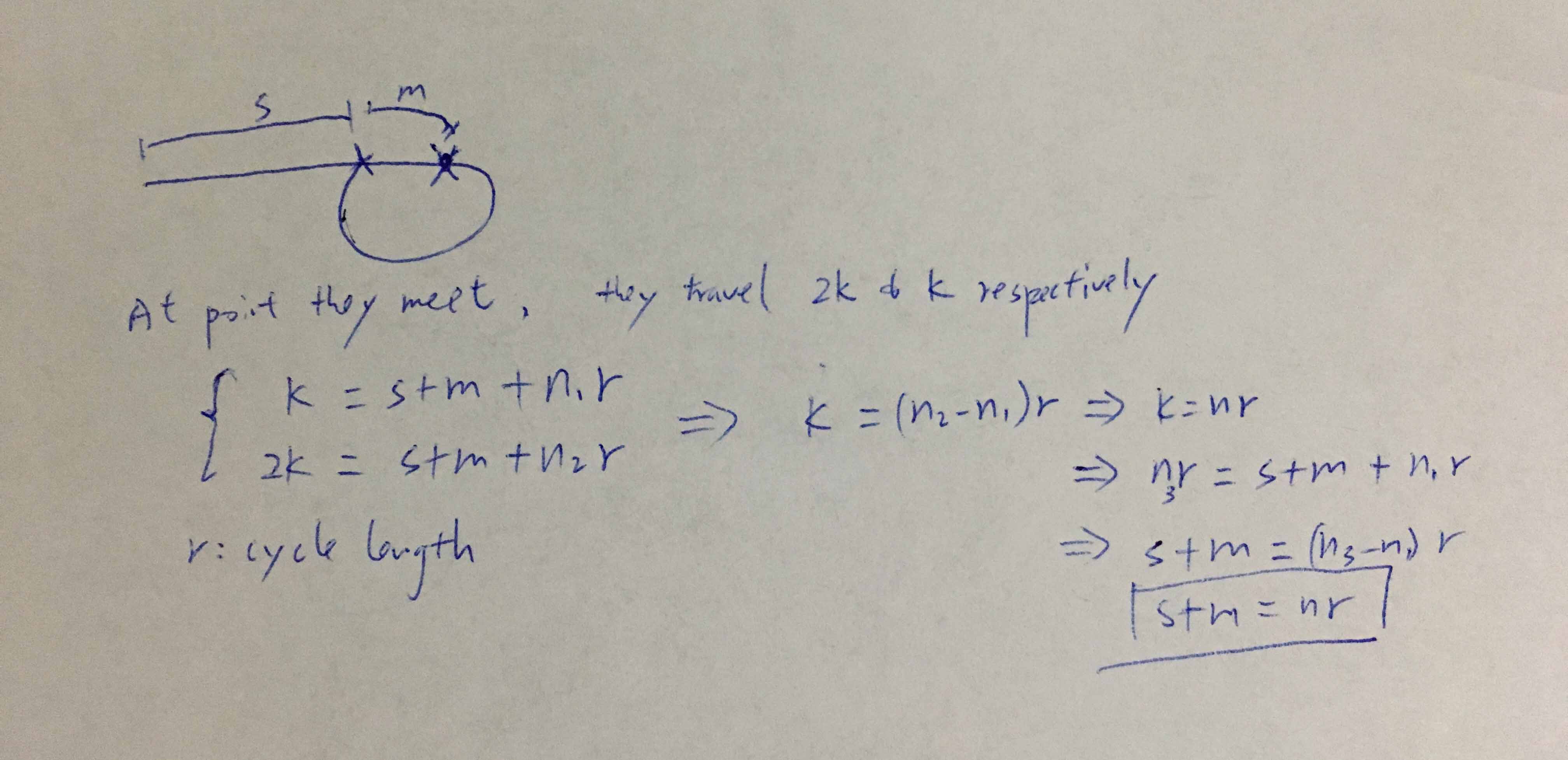
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head, fast = head;
while(fast!= null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(fast==slow) break;
}
if(fast==null || fast.next==null) return null; //no cycle
//this time both at the same speed
slow = head;
while(fast!=slow){
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
The cycle detection technique is sometimes used to solve other problem:
287. Find the Duplicate Number
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
public int findDuplicate(int[] nums) {
int slow = 0, fast = 0;
do {
slow = nums[slow];
fast = nums[fast]; fast = nums[fast];
} while(slow != fast);
slow = 0;
while(slow!=fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
String Search
159. Longest Substring with At Most Two Distinct Characters
3. Longest Substring Without Repeating Characters
395. Longest Substring with At Least K Repeating Characters (this is a bit of variation, find the longest substring of given #unique char, if #unique char ==#uniqueCharItsCountGreaterEqK, it is solution candidate. #unique char is possible to be 1-26, we just try all possibility) Find a substring that its # unique characters == k can use below template methodology.
Two pointer template: template that can solve most 'substring' problems
Idea: proceed with the end pointer if the condition(s) maintains. When the condition(s) break(s), move the begin pointer until it restores the conditions (of course update the information when we move begin pointer).
Repeat until end of string S:
move the end pointer and update conditions
while conditions mismatch
move the start pointer and update conditions
Now the conditions are correct with (begin, end), calculate the solution length and update max/min if appropriate
int findSubstring(string s){
vector<int> map(128,0);
int counter; // check whether the substring is valid
int begin=0, end=0; //two pointers, one point to tail and one head
int d; //the length of substring
for() { /* initialize the hash map here */ }
while(end<s.size()){
if(map[s[end++]]-- ?){ /* modify counter here */ }
while(/* counter condition */){ //restore the conditions
/* update d here if finding minimum*/
//increase begin to make it invalid/valid again
if(map[s[begin++]]++ ?){ /*modify counter here*/ }
}
/* update d here if finding maximum*/
}
return d;
}
Two Sum Problem
If the array is sorted, we can use two pointers to scan the list once to solve two sum problem.
For three sum, just reduce it to two sum by fixing one number.
But not necessarily fixing the number from left to right (smallest to largest), it could be from right to left (largest to smallest) depending on the problem need.
This is of the same nature of 2 sum problem but there are duplicated elements... and corner cases.
Sliding Window
Given two strings s1 and s2, write a function to return true if s2 contains the permutation of s1.
In other words, one of the first string's permutations is the substring of the second string.
This problem can be solved by char counting, and use cancellation, check if all count is zero when the window slides. The running time is still O(n) with a constant c=26. Note: if we compare count iterating through s1, then the running time is depending on length of s1, it will be O(nm).
The optimal solution will be using two pointer with sliding window:
- whenever we see a count >0, means the char is not the one in s1 / there is excess of that character.
- restore the counting/criteria by moving the left boundary of the sliding window.
- when sliding window length is == m, this is the substring we want. This is only possible when the substring contains exactly the same char count as s1. (not running into condition 1)
Sorted Array, Two Pointer Methodology Helps to Eliminate Unnecessary Subproblem/Comparison
This problem, when we have no ideas how to solve, try to think from brutal force solution and see how to optimize.
In brutal force, we get one element from each list, and the range will be the max - min among these elements. But the list is sorted, some comparisons are not necessary and they must be of larger range.
Then the problem becomes how we make use of the sorted array.