Segment Tree

Segment tree can be implemented to find range sum or range minimum, depending on the problems.

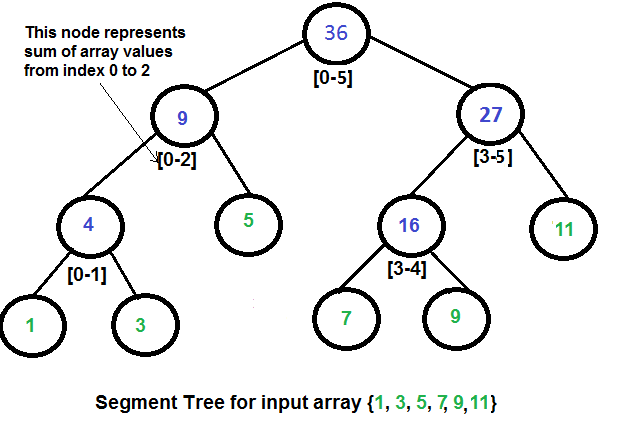
307. Range Sum Query - Mutable

Build tree: O(n) as there are total 2n-1 nodes, and value of every node is calculated only once in tree construction. It is full binary tree except the leave level, so, number of nodes = 2^(log2n +1) -1 = 2n -1

Query and Update: O(logn)

When the update and query frequency is more or less the same, this is better than pre-computed sum(j) - sum(i) approach.

class NumArray {

    private class SegmentTreeNode {
        int begin, end, sum;
        SegmentTreeNode left, right;

        public SegmentTreeNode(int begin, int end) {
            this.begin = begin;
            this.end = end;
            left = right = null; sum = 0;
        }
    }

    private SegmentTreeNode buildTree(int[] nums, int begin, int end) {
        SegmentTreeNode root = new SegmentTreeNode(begin, end);
        if(begin==end) {
            root.sum = nums[begin];
        } else {
            int mid = begin + (end-begin)/2;
            root.left = buildTree(nums, begin, mid);
            root.right = buildTree(nums, mid+1, end);
            root.sum = root.left.sum + root.right.sum;
        }

        return root;     
    }

    private void update(SegmentTreeNode root, int pos, int val) {
        if(root.begin == root.end) {
            root.sum = val;
        } else {
            int mid = root.begin + (root.end-root.begin)/2;
            if(pos<=mid) 
                update(root.left, pos, val);
            else
                update(root.right, pos, val);
            root.sum = root.left.sum + root.right.sum;
        }
    }

    private int sumRange(SegmentTreeNode root, int begin, int end) {
        if(root.begin == begin && root.end==end) {
            return root.sum;
        } else {
            int mid = root.begin + (root.end-root.begin)/2;
            if(end<=mid) 
                return sumRange(root.left, begin, end);
            else if (begin>mid)
                return sumRange(root.right, begin, end);
            else
                return sumRange(root.left, begin, mid) + sumRange(root.right, mid+1, end);
        }
    }

    private SegmentTreeNode root;

    public NumArray(int[] nums) {
        if(nums!=null && nums.length>0)
            root = buildTree(nums, 0, nums.length-1);
    }

    public void update(int i, int val) {
        update(root, i, val);
    }

    public int sumRange(int i, int j) {
        return sumRange(root, i, j);
    }
}