Binary Indexed Tree

Binary Indexed Tree require linear memory space.
Binary Indexed Trees are very easy to code.
You can use it as an n-dimensional data structure.

Storing the cumulative sum of all the values including that node and its left subtree. For example, given our values, we would store the following:

Before:
[ +5] [ +1] [+15] [+11] [+52] [+28] [ +0]
  1     2     3     4     5     6     7

After:
                 4
               [+32]
              /     \
           2           6
         [ +6]       [+80]
         /   \       /   \
        1     3     5     7
      [ +5] [+15] [+52] [ +0]

If we convert from this to a binary indexed tree, we can observe that the subtraction / add of the last set bit of current index is essentially following the right left or right child/parent links. (for update and query)

There are at most logn nodes to deal with, so it is O(logn) for both update and query.

                100
               [+37]
              /     \
          010         110
         [+11]       [+80]
         /   \       /   \
       001   011   101   111
      [+10] [+15] [+52] [ +0]

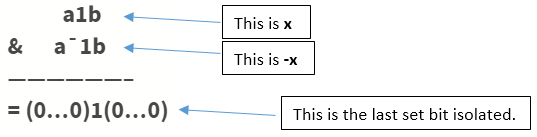
To find the last set bit: x & (-x)

Intuition:

Say x = a1b(in binary) is the number whose last set bit we want to isolate.

-x= 2’s complement of x =(a1b)’+ 1 =a’0b’+ 1 =a’0(0….0)’ + 1=a’0(1...1) + 1=a’1(0…0)=a’1b

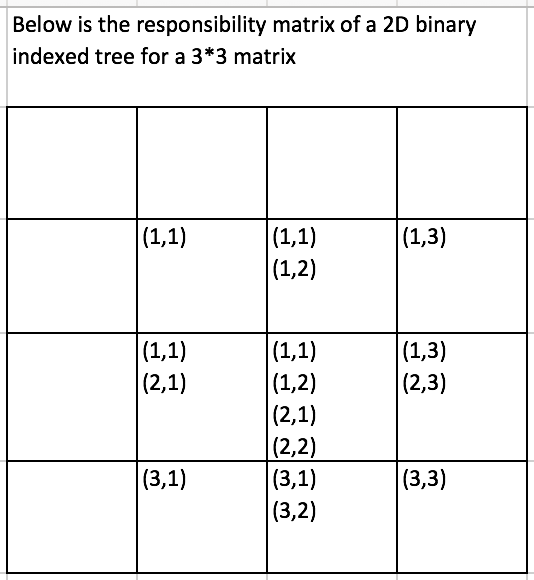
2-dimensional Binary Index Tree Example

308. Range Sum Query 2D - Mutable

The same algorithm is still working fine but with some changes.

The sum should be computed as below:

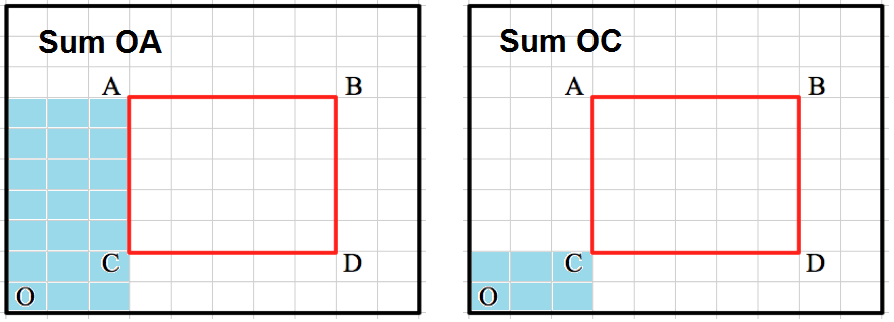
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC)

For example, to get sumRegion(1,1) to (3,3) = (3,3) + (3,2) + (2,3) + (2,2)

public class NumMatrix {
    int[][] tree;
    int[][] nums;
    int m, n;

    public NumMatrix(int[][] matrix) {
        if(matrix==null || matrix.length==0 || matrix[0].length==0) return;
        m = matrix.length;
        n = matrix[0].length;
        tree = new int[m+1][n+1];
        nums = new int[m][n];
        for (int i=0; i<m; i++) {
            for(int j=0; j<n; j++) {
                update(i, j, matrix[i][j]);
            }
        }
    }

    public void update(int row, int col, int val) {
        int delta = val - nums[row][col];
        nums[row][col] = val;
        for(int i=row+1; i<=m; i+=i&(-i)) { //since it is base 1 arrary
            for(int j=col+1; j<=n; j+=j&(-j)) {
                tree[i][j] += delta;
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        //because of base 1 arrary of tree[][]
        return sum(row2+1, col2+1) - sum(row1, col2+1) - sum(row2+1, col1) + sum(row1, col1); 
    }

    public int sum(int row, int col) {
        int sum = 0;
        for(int i=row; i>0; i-=i&(-i)) { //since it is base 1 arrary
            for(int j=col; j>0; j-=j&(-j)) {
                sum += tree[i][j];
            }
        }

        return sum;
    }

    // time should be O(log(m) * log(n))
}

A more realistic solution during interview...

Though the run time split is update: O(m), query O(n) which is not as good as O(logm*logn) in BIT case.

public class NumMatrix {
    private int[][] colSum;
    private int[][] matrix;    

    public NumMatrix(int[][] matrix) {
        if(matrix==null || matrix.length<1 || matrix[0].length<1) return;
        int m = matrix.length, n = matrix[0].length;
        this.matrix = matrix;

        //calculate column sum
        colSum = new int[m+1][n];
        for(int i=1; i<=m; i++) {
            for(int j=0; j<n; j++) {
                colSum[i][j] = colSum[i-1][j] + matrix[i-1][j];
            }
        }
    }

    //worst case is O(m) that we update all the row
    public void update(int row, int col, int val) {
        for(int i=row+1; i<colSum.length; i++) {
            colSum[i][col] = colSum[i][col] - matrix[row][col] + val;
        }
        matrix[row][col] = val;
    }

    //worst case is O(n) that we need to iterate through all columns
    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for(int j=col1; j<=col2; j++) {
            sum += colSum[row2+1][j] - colSum[row1][j];
        }
        return sum;
    }
}

Binary Indexed Tree

Binary Indexed Tree

2-dimensional Binary Index Tree Example

results matching ""

No results matching ""