Max Flow

https://www.geeksforgeeks.org/max-flow-problem-introduction/

https://www.geeksforgeeks.org/ford-fulkerson-algorithm-for-maximum-flow-problem/

https://www.geeksforgeeks.org/dinics-algorithm-maximum-flow/

Maximum flow problems involve finding a feasible flow through a single-source, single-sink flow network that is maximum.
Let’s take an image to explain how above definition wants to say.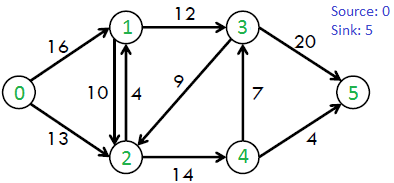

Each edge is labeled with a capacity, the maximum amount of stuff that it can carry. The goal is to figure out how much stuff can be pushed from the vertex s(source) to the vertex t(sink).

maximum flow possible is : 23

Edmonds-Karp Algorithm

The idea of Edmonds-Karp is to use BFS in Ford Fulkerson implementation as BFS always picks a path with minimum number of edges. When BFS is used, the worst case time complexity can be reduced to O(VE^2).

Proof: https://www.cs.cornell.edu/courses/cs4820/2012sp/handouts/edmondskarp.pdf

Dinic’s Algorithm

In Dinic’s algorithm, we use BFS to check if more flow is possible and to construct level graph. In level graph, we assign levels to all nodes, level of a node is shortest distance (in terms of number of edges) of the node from source. Once level graph is constructed, we send multiple flows using this level graph.

Applications

UVA - 11082 Matrix Decompressing

https://blog.csdn.net/Fire_to_cheat_/article/details/81034263

题意:定义一个R*C的正整数矩阵（1<=R,C<=20),设Ai为前i行所有元素之和，Bi为前i列所有元素之和。

题目已知R,C和数组A，B。要找一个满足条件的矩阵。矩阵中的元素要满足(1<=X[i][j]<=20)。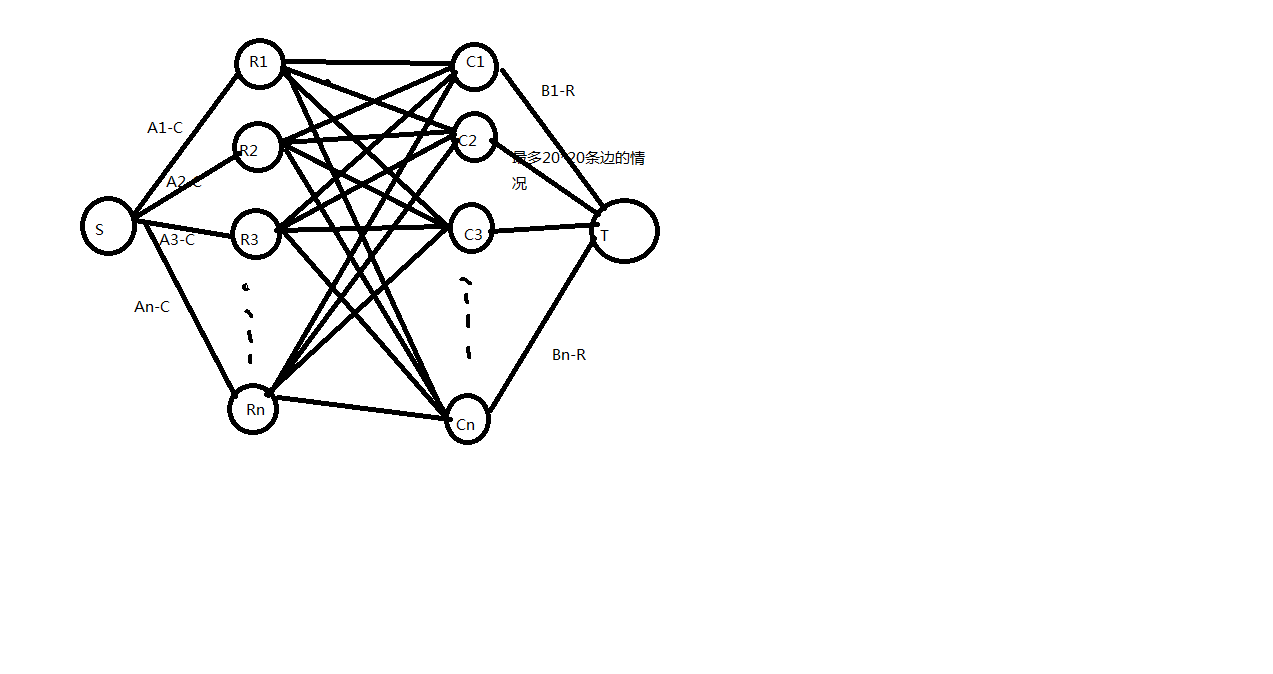

//https://blog.csdn.net/Fire_to_cheat_/article/details/81034263
//https://www.geeksforgeeks.org/ford-fulkerson-algorithm-for-maximum-flow-problem/
public class MatrixDecompressing {
    private static int R, C;

    public static void main(String[] args) {
        R = 3;
        C = 4;
        int a[] = {10, 31, 58};
        int b[] = {10, 20,37, 58};

        int c[] = new int[a.length]; c[0] = a[0] - C;
        int d[] = new int[b.length]; d[0] = b[0] - R;
        for(int i=1; i<a.length; i++) {
            c[i] = a[i] - a[i-1] - C; //because we set cap as 0-19, we need to subtract 1 from each entries
        }
        for(int i=1; i<b.length; i++) {
            d[i] = b[i] - b[i-1] - R;
        }

        int[][] graph = new int[R+C+2][R+C+2];
        int s = 0, t = R+C+1;
        for(int i=0; i<R; i++) {
            graph[s][i+1] = c[i];
        }
        for(int i=0; i<C; i++) {
            graph[R+i+1][t] = d[i];
        }
        for(int i=1; i<=R; i++) {
            for(int j=1; j<=C; j++) {
                graph[i][R+j] = 19;
            }
        }

        System.out.println(maxFlow(graph, s, t));

    }

    static boolean bfs(int[][] rGraph, int s, int t, int[] parent) {
        boolean visited[] = new boolean[R+C+2];
        Queue<Integer> q = new LinkedList<>();
        q.add(s);
        visited[s] = true;
        parent[s] = -1;
        while(!q.isEmpty()) {
            int u = q.poll();
            for(int v=0; v<R+C+2; v++) {
                if(!visited[v] && rGraph[u][v] > 0) {
                    q.add(v);
                    parent[v] = u;
                    visited[v] = true;
                }
            }
        }

        return visited[t]==true;

    }

    static int maxFlow(int graph[][], int s, int t) {
        int u, v;
        int[][] rGraph = new int[R+C+2][R+C+2];
        for(u=0; u<R+C+2; u++) {
            for(v=0; v<R+C+2; v++) {
                rGraph[u][v] = graph[u][v];
            }
        }

        int parent[] = new int[R+C+2];
        int max_flow = 0;
        while(bfs(rGraph, s, t, parent)) {
            int path_flow = Integer.MAX_VALUE;
            for(v=t; v!=s; v=parent[v]) {
                u = parent[v];
                path_flow = Math.min(path_flow, rGraph[u][v]);
            }

            //update rGraph  & reverse edges along the path
            for(v=t; v!=s; v=parent[v]) {
                u=parent[v];
                rGraph[u][v] -=path_flow;
                rGraph[v][u] +=path_flow;
            }

            max_flow += path_flow;
        }

        //print the matrix
        for(int i=1; i<=R; i++) {
            for(int j=1; j<=C; j++) {
                System.out.print(19-rGraph[i][R+j]+1 + "\t");
            }
            System.out.println();
        }
        return max_flow;
    }

}